Mathematik inklusiv lehren lernen

Entwicklung eines forschungsbasierten interdisziplinären Fortbildungskonzepts

Susanne Prediger, Jan Kuhl, Christian Büscher & Sarah Buró

Journal für Psychologie, 27(2), 288–312

https://doi.org/10.30820/0942-2285-2019-2-288www.journal-fuer-psychologie.de

Zusammenfassung

Für die Qualitätsentwicklung im inklusiven Fachunterricht der Sekundarstufe 1 liegen zwar bewährte Unterrichtskonzepte und substanzielle empirische Befunde aus Psychologie, Sonderpädagogik und Fachdidaktik vor, jedoch keine Fortbildungskonzepte, in denen diese Befunde und Konzepte interdisziplinär integriert und handlungsnah aufbereitet sind. Der Artikel stellt die Entwicklung eines forschungsbasierten interdisziplinären Fortbildungskonzepts für Regelschullehrkräfte und Förderlehrkräfte vor, das die qualitative Erhebung von inklusionsbezogenen Lehrendenperspektiven zum Ausgangspunkt für die Spezifizierung und Perspektivierung der Fortbildungsgegenstände macht. Dazu gibt er exemplarische Einblicke in das zugrundeliegende Design-Research-Projekt, in dem das Fortbildungskonzept in drei Designexperimentzyklen iterativ entwickelt, erprobt und untersucht wurde. Er stellt zudem das daraus erwachsene Fortbildungskonzept vor: In fünf Fortbildungssitzungen wird fallbezogen ein integratives Handlungskonzept erarbeitet und am Beispiel einer Unterrichtseinheit zu Prozenten mit den Teilnehmenden der Fortbildung erprobt. Die Fortbildung befähigt die Lehrkräfte, für die Lernvoraussetzungen mathematisches Vorwissen, Sprachkompetenz, Arbeitsgedächtnis und Strategienutzung/metakognitive Regulation jeweils Anforderungen zu identifizieren, differenzierte Schwerpunkte zu setzen, fokussiert zu fördern sowie gemeinsames Lernen zu initiieren.

Schlüsselwörter: Inklusion, inklusiver Mathematikunterricht, gegenstandsbezogenes Expertisemodell, didaktische Anforderungssituationen, Fortbildungskonzept

Summary
Learning to teach mathematics inclusively: Development of a research-based interdisciplinary professional development program

For quality development in inclusive subject matter classrooms of middle schools, there exist inclusive instructional approaches and empirical findings from psychology, special needs education, and subject matter didactics. However, programs for professional develoment (PD) are still missing which integrate these findings and approaches in an interdisciplinary and situated way. The article presents the development of a research-based interdisciplinary professional development program for mathematics teachers and special needs teachers that started from qualitative investigations of teachers’ perspectives for specifying what teachers should learn and in which perspective they should do so. The article provide insights into the underlying design research project in which the PD program was iteratively developed, tested, and investigated. The developed PD program for teaching mathematics inclusively is presented: Within five case-based PD sessions, participating teachers work on an integrated instructional approach and collectively experiment with it for the case of an inclusive teaching unit for percentages. The PD program empowers the teachers to (a) identify demands for four relevant learning prerequisites (mathematical understanding, language proficiency, working memory and strategies/metacognitive regulation), (b) set differentiated priorities, (c) support students adaptively and (d) orchestrate joint learning situations.

Key words: inclusion, inclusive mathematics classrooms, model of content-related expertise, situational demands, professional development program

Um die Systemumstellung zu inklusiven Schulen auch durch entsprechende Qualitätsentwicklung im Fachunterricht zu begleiten, ist eine Professionalisierung von Regelschullehrkräften und sonderpädagogischen Lehrkräften für den inklusiven Fachunterricht notwendig. Dies ist in der Sekundarstufe 1 allerdings bislang ein oft nur konstatiertes Desiderat (Döbert und Weishaupt 2013; Scherer et al. 2016). Mathematik eignet sich als Fach für die Entwicklung eines forschungsbasierten Fortbildungskonzepts, da auf Individual- und Unterrichtsebene bereits substanzielle Befunde und Konzepte aus Psychologie, Sonderpädagogik und Fachdidaktik für individuelle Förderung und inklusiven Fachunterricht vorliegen, die in Fortbildungskonzepte eingespeist werden können. Doch wurden diese bislang noch kaum interdisziplinär integriert und zu Forschungsbefunden über inklusionsbezogene Lehrendenperspektiven in Beziehung gesetzt. Dies erfolgt aktuell im BMBF-Projekt »Matilda – Mathematik inklusiv lehren lernen« (Projektleitung S. Prediger und J. Kuhl). Das Fortbildungskonzept ist forschungsbasiert, da es den derzeitigen wissenschaftlichen Erkenntnisstand berücksichtigt und durch seine gleichzeitige Beforschung auch erweitert. Dies geschieht, indem es

inhaltlich die Ergebnisse von Forschung zu individuellen Lernvoraussetzungen, individuellen Förderkonzepten und inklusiven Unterrichtskonzepten aufgreift;

Forschung zu notwendigem inklusionsbezogenem Professionswissen von Lehrkräften und typische Lehrendenperspektiven einbezieht und selbst durchführt, um Fortbildungsgegenstände zu gewichten und zu perspektivieren;

themenübergreifend beforschte Gestaltungsprinzipien für Fortbildungen gegenstandsbezogen umsetzt;

die Fortbildungssequenzen nach Analyse der initiierten Professionalisierungsprozesse optimiert; und

das Fortbildungsangebot in Bezug auf die Wirksamkeit für professionelle Kompetenz von Lehrkräften und die Leistungen der Schülerinnen und Schüler untersucht.

Dieser Artikel fokussiert auf Zugang A-C, während die weiteren Zugänge in späteren Publikationen vertieft werden. Dazu wird in Abschnitt 1 und 2 der Forschungsstand dargestellt und in Abschnitt 3 die Methoden der Design-Research-Studie erläutert, mit denen dieser ergänzt und gewichtet wird. Abschnitt 4 gibt erste Einblicke in ein zentrales Forschungsergebnis und damit in die Entwicklung eines solchen forschungsbasierten Fortbildungskonzepts.

Forschungsstand mit relevanten Befunden und Konzepten auf Unterrichtsebene

Strategien inklusiven Unterrichts: Unterstützungs- und Förderstrategien

Inklusiver Unterricht wird hier verstanden als ein nichtaussondernder Unterricht (Prengel 2007; Wember 2013), der vielfältige Fähigkeitsprofile im gesamten Leistungsspektrum berücksichtigt, bis hin zum sonderpädagogischen Förderbedarf Lernen und Geistige Entwicklung und dabei viele Heterogenitätsaspekte einbezieht. Angestrebt wird eine Balance zwischen individuellem und gemeinsamen Lernen, die einerseits die Einzelnen gemäß ihrer je spezifischen Profile fördert und andererseits gemeinsames Lernen ermöglicht. Gemeinsames Lernen hat sowohl eine soziale Dimension im Sinne der sozialen Teilhabe (Wild et al. 2015; Spörer, Maaz, Vock, Schründer-Lenzen und Luka 2015), aber auch eine fachliche Dimension im Sinne des Von- und Miteinander-Lernens (Wocken 1998; Häsel-Weide und Nührenbörger 2013).

Zur Fundierung des individuellen Lernens wurden in der Sonderpädagogik verschiedene Ansätze zur individuellen Förderung mathematischer Kompetenzen im Grundschulalter entwickelt, am meisten für den Förderschwerpunkt Lernen (z. B. Kutzer 1999; Sinner und Kuhl 2010) und deutlich weniger für den Förderschwerpunkt Geistige Entwicklung (Ratz 2009; Kuhl, Sinner und Ennemoser 2012). Diese Ansätze auf die Sekundarstufe zu übertragen bedarf weiterer Forschungs- und Entwicklungsarbeit (z. B. in Moser Opitz et al. 2017). International liegen zwar mehr Arbeiten zur individuellen Förderung von Lernenden mit Lernschwierigkeiten und auch intellektueller Beeinträchtigung im Inhalts- und/oder Altersbereich der Sekundarstufe I vor (vgl. Metaanalyse von Gersten et al. 2009; Misquitta 2011), trotzdem besteht auch hier noch erheblicher Forschungsbedarf. In der Mathematikdidaktik ist Heterogenität seit den 1980er Jahren ein wichtiges Thema vieler Entwicklungs- und Forschungsprojekte, gerade bzgl. offen differenzierender Settings, die dem gemeinsamen Lernen zugrunde liegen können und bzgl. Förderkonzepten für mathematisch Schwache (vgl. Überblick in Scherer et al. 2016).

Konzepte für gemeinsames Lernen (z. B. Feuser 1989; Wocken 1998) wurden fachdidaktisch bislang nur für die Grundschule konkret entwickelt (Scherer et al. 2016; Häsel-Weide und Nührenbörger 2013). Oft standen Unterstützungsstrategien für das Zugänglichmachen durch Anpassen an individuelle Lernvoraussetzungen im Vordergrund, zum Beispiel im Universal Design for Learning (CAST 2011), weniger dagegen Förderstrategien, deren Grundlagen in Abschnitt 1.3 vorgestellt werden.

Forschung zu Lernenden und individuellen Lernvoraussetzungen

Um mögliche Förder- und Unterstützungsbedarfe aller Lernender zu identifizieren, eignet sich das »Modell der kognitiven und motivationalen-volitionalen individuellen Voraussetzungen erfolgreichen Lernens« (INVO-Modell) von Hasselhorn und Gold (2009).

Auf Basis vieler Befunde der psychologischen Lehr-Lern-Forschung stellen die Autoren fünf Lernvoraussetzungen für erfolgreiches Lernen heraus: Vorwissen, Arbeitsgedächtnis, Strategienutzung/metakognitive Regulation, Motivation und Selbstkonzept sowie Volition und lernbegleitende Emotion. Lernstörungen entstehen in der Interaktion von individuellen Voraussetzung und Umweltbedingungen wie dem häuslichen Umfeld (Kuhl 2019). Didaktisch-methodische Entscheidungen zur Förderung werden möglichst an den individuellen Voraussetzungen der Lernenden orientiert, die Umweltbedingungen dabei im Hintergrund mitberücksichtigt.

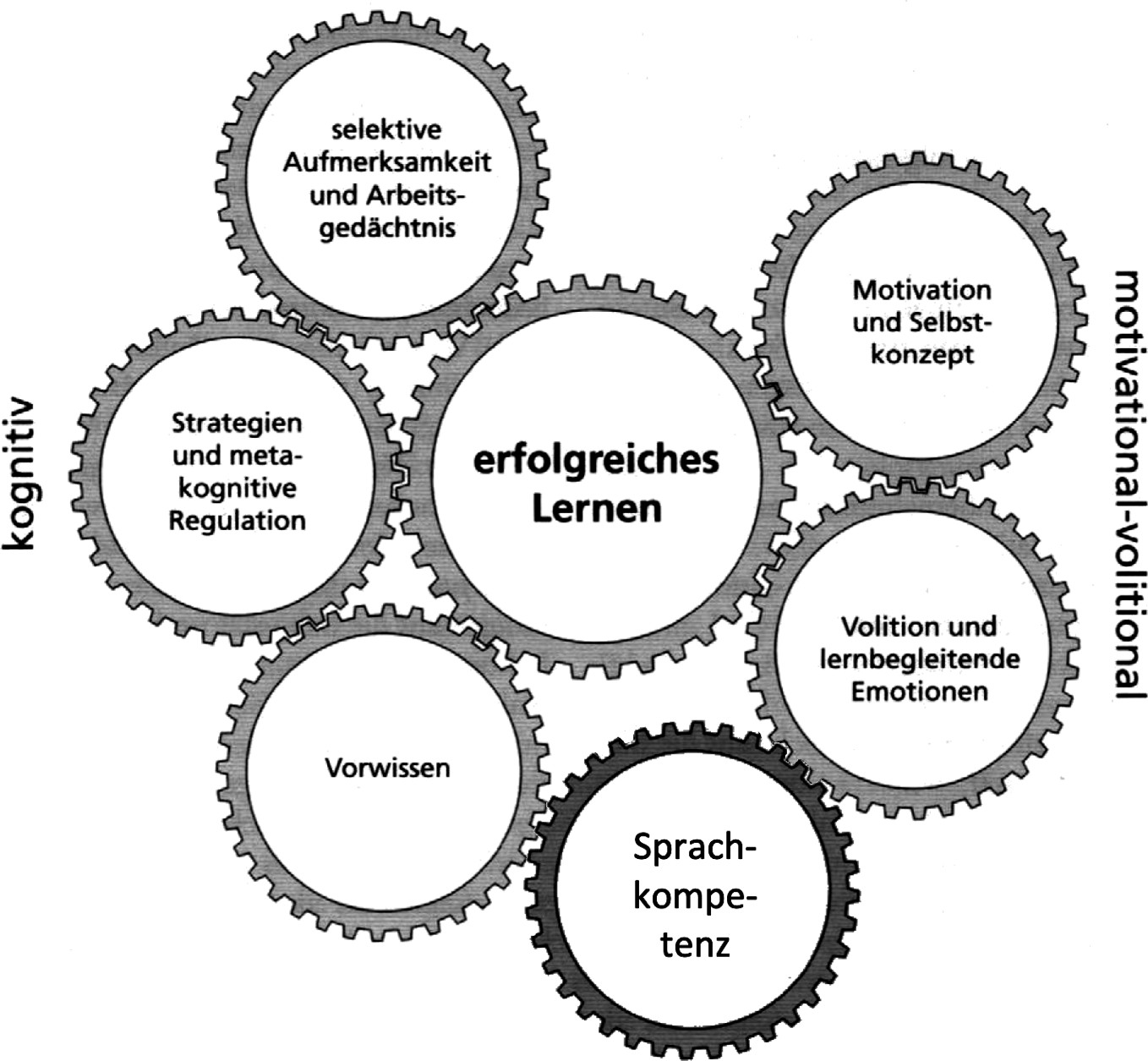
Abbildung 1: Kategorien für individuelle Lernvoraussetzungen (Hasselhorn und Gold 2009, ergänzt um Sprachkompetenz in Prediger et al. 2019)

In Abbildung 1 ergänzen wir Sprachkompetenz als weitere Lernvoraussetzung, die zwar auch unter Vorwissen subsumiert werden könnte, doch für Mathematikunterricht von mathematischem Vorwissen getrennt aufzuführen ist. Im mathematischen Lernprozess eingeschränkt sind sprachlich schwache Lernende empirisch nachweislich nicht nur im Förderschwerpunkt Sprache, sondern auch zum Beispiel im Förderschwerpunkt Lernen, bei sozialer Benachteiligung oder Zuwanderung (Lütje-Klose 2012).

Das erweiterte INVO-Modell bietet damit ein einheitliches Kategoriensystem für alle Lernenden, das individuelle Diagnosen auf einem Kontinuum ermöglicht und pauschale Gruppenzuschreibungen aufweichen kann.

Fachdidaktische Lernstufungen für entwicklungslogisch strukturierte Förderstrategien

Das INVO-Modell beschreibt, worin sich schwache Lernende von starken Lernenden unterscheiden. Um diesen Unterschieden gerecht zu werden, muss Unterricht adaptiv gestaltet werden, das heißt an die individuellen Voraussetzungen angepasst werden. Die Anpassung kann durch zwei verschiedene Strategien erfolgen, die je nach Lernvoraussetzung ausgewählt werden (Wember 2013):

Bei der Unterstützungsstrategie werden fehlende Lernvoraussetzungen umgangen, indem Arbeitsprozesse adaptiv entlastet oder unterstützt werden. Sinnvoll ist dies insbesondere für kaum förderbare Lernvoraussetzungen wie dem Arbeitsgedächtnis, welches zum Beispiel durch übersichtliche Arbeitsblattgestaltung entlastet werden kann (Krajewski und Ennemoser 2010; CAST 2011). Analog zielen Unterstützungsstrategien für eingeschränkte Sprachkompetenzen auf adaptive Reduktion sprachlicher Anforderungen (Lütje-Klose 2012).

Bei der Förderstrategie dagegen werden fehlende Lernvoraussetzungen direkt gefördert, um Anschlussfähigkeit an spätere Anforderungen zu erzielen (Wember 2013). Dies ist sowohl bzgl. einiger sprachlicher Anforderungen als auch bzgl. zentraler Elemente des mathematischen Vorwissens zentral, denn Wissenszuwachs in der Mathematik ist hoch kumulativ. Eine solche Förderung kann auch als entwicklungsniveaubezogene Differenzierung (Feuser 1989; Prediger und von Aufschnaiter 2017) erfolgen.

Für die Umsetzung der Förderstrategie ist aus fachdidaktischer und sonderpädagogischer Sicht entscheidend, die Lernstruktur und Entwicklungslogik des jeweiligen Lerngegenstands zu identifizieren (Kuhl, Hecht und Euker 2016 aus sonderpädagogischer Sicht; Prediger und von Aufschnaiter 2017 aus fachdidaktischer Sicht). So bildet zum Beispiel im Kompetenzentwicklungsmodell von Krajewski (2013) die Entwicklung der Zahl-Größen-Verknüpfung die Grundlage für die Grundschularithmetik. Ohne das Verständnis für grundlegende Konzepte, wie etwa das additive Teil-Ganzes-Konzept, können nachfolgende Lernstufen nicht zufriedenstellend bewältigt werden (Krajewski 2013). Für die Sekundarstufe 1 hat Moser Opitz (2007) die typischen Elemente solcher unüberspringbaren Lernstufungen identifiziert: Sie liegen einerseits in Verstehensgrundlagen wie dem Stellenwert- und Operationsverständnis, andererseits in zu automatisierendem Basiskönnen wie dem Zählen in Schritten. Dabei zeigen sich verschleppte Schwierigkeiten im Bereich dieser Verstehensgrundlagen bei lernschwachen Lernenden noch bis in die Klasse 8/9; dort behindern sie die Aufnahme späterer Lerninhalte (Ennemoser, Krajewski und Schmidt 2011; Moser Opitz 2007).

Forschungsstand zur inklusionsbezogenen Expertise und Professionalisierung

Orientierungen und Anforderungssituationen

Empirische Studien zur professionellen inklusionsbezogenen Kompetenz von Lehrkräften sind in Deutschland noch rar und nach dem Review-Artikel von Melzer et al. (2015) vor allem auf generelle Haltungen zur Inklusion bezogen. Generelle Haltungen alleine reichen allerdings für die Gestaltung von Unterricht nicht aus, weil sie noch nicht zum Handeln befähigen, wie die Meta-Analyse zu Lehrkräften von Scruggs und Mastropieri (1996) zeigt.

Für eine genauere Bestimmung der Fortbildungsgegenstände werden gemäß des Reviews von Melzer et al. (2015) unterschiedliche Anforderungssituationen identifiziert und strukturiert, zum Beispiel bei Moser und Kropp (2014) folgende sieben Anforderungsbereiche: Lernstands- und Entwicklungsdiagnostik, Beratung und Organisation, Lern- und Entwicklungsförderung, Binnendifferenzierte Unterrichtung, Behinderungsspezifische Kommunikation, Interdisziplinäre Kooperation und Förderung des sozialen Lernens.

Der vorliegende Artikel fokussiert auf die Anforderungsbereiche Binnendifferenzierung sowie Lern- und Entwicklungsförderung, die auch in anderen Ansätzen zentral im Überschneidungsbereich für Regel- und Förderlehrkräfte liegen. Für diese Anforderungsbereiche werden im Folgenden die notwendigen Komponenten professioneller Expertise genauer spezifiziert, um die notwendigen Fortbildungsgegenstände zu bestimmen.

Gegenstandsbezogenes Expertisemodell und Forschungslücken

Um die Anforderungsbereiche Binnendifferenzierung sowie Lern- und Entwicklungsförderung genauer auszudifferenzieren, wird in diesem Artikel auf ein gegenstandsbezogenes Expertisemodell zurückgegriffen, das sich an Bromme (1992) anlehnt und für gegenstandsbezogene Professionalisierungsforschung adaptiert wurde (Prediger 2019). Nach Bromme (1992) erfolgt die Konzeptualisierung von Lehrkräfte-Expertise ausgehend von typischen Anforderungssituationen und den Praktiken der Lehrkräfte, diese zu bewältigen:

Dabei sind Didaktische Anforderungssituationen (bzw. kurz Jobs) typische Konstellationen im Unterrichtsgeschehen, die eine Lehrkraft zur Erreichung der übergeordneten Ziele bewältigen muss.

Orientierungen sind gegenstandsübergreifende oder -bezogene Haltungen, die die Priorisierungen und Interpretationen der Lehrkräfte zur jeweiligen Anforderungssituation implizit oder explizit prägen und damit den Praktiken zugrunde liegen. Darunter fallen zum Beispiel generelle Haltungen zum Unterrichtsgegenstand oder zu Lernprozessen, aber auch individuelle Qualitätskriterien für inklusiven Unterricht.

Denk- und Wahrnehmungskategorien betreffen das konzeptuelle, nicht-propositionale Wissen, das die kategoriale Wahrnehmung und die Denkweisen der Lehrkräfte filtert und damit ihre Praktiken fokussiert.

Mit dem gegenstandsbezogenen Expertisemodell wird für ausgewählte Anforderungssituationen empirisch rekonstruiert, wie Lehrkräfte diese Anforderungssituationen bewältigen und welche Orientierungen und Kategorien ihren Praktiken zugrunde liegen (Prediger 2019). Diese Job-Analyse gilt »als Heuristik bei der Suche nach den ›natürlichen‹ Kategorien des Expertenwissens« (Bromme 1992, 88).

Die pädagogische und sonderpädagogische Forschungsliteratur identifiziert Denk- und Wahrnehmungskategorien für die Anforderungsbereiche Binnendifferenzierung sowie Lern- und Entwicklungsförderung vor allem im Wissen zu unterschiedlichen Förderschwerpunkten und generellen Haltungen (vgl. Überblick in Döbert und Weishaupt 2013) oder bei fachunabhängigen Praktiken zur Individualisierung (Schuppener 2014). Allerdings weist die (auf inklusiven Mathematikunterricht der Grundschule bezogene) Interviewstudie von Korff (2015) und die Erhebung zum Professionswissen von Jandl (2016) darauf hin, dass diese unbedingt mit fachdidaktischen Perspektiven verknüpft sein sollten, um handlungswirksam die Unterrichtsqualität des inklusiven Mathematikunterrichts zu heben (ähnlich Lütje-Klose, Miller und Ziegler 2014 für andere Fächer). Dies korrespondiert mit allgemeinen Befunden zur Lehrerbildungsforschung (Lipowsky und Rzejak 2017), die Fachbezug von Fortbildungen als zentrale Gelingensbedingung herausarbeitet.

Wenig ist jedoch darüber bekannt, welche Denk- und Wahrnehmungskategorien und konkreteren Orientierungen aus dem deutlich zu breiten Forschungs- und Theoriestand tatsächlich für Lehrkräfte am relevantesten sind. Diese müssen daher für das hier beschriebene Projekt zunächst identifiziert werden.

Ziele und Anlage des übergreifenden Projekts Matilda

Ausgangspunkt des Forschungsprojekts sind die erheblichen Forschungsdesiderate in Bezug zur Frage der Verknüpfungen von fachlicher, fachdidaktischer und sonderpädagogischer Expertise von Lehrkräften zum Zwecke der Planung und Umsetzung eines qualitativ hochwertigen inklusiven Unterrichts (Döbert und Weishaupt 2013). Das in Matilda entwickelte Fortbildungskonzept stellt diese Verknüpfung daher exemplarisch an einer Unterrichtseinheit her: Die Unterrichtseinheit »Prozente verstehen« in Klasse 7 ist mit Blick auf Lernende des Regelspektrums im vorangegangenen Design-Research-Projekt auf Unterrichtsebene entwickelt und evaluiert (Pöhler 2018) und danach bzgl. Zugänglichkeit für Lernende mit Förderschwerpunkt Lernen weiterentwickelt worden (Pöhler, Prediger und Strucksberg 2018). Die Unterrichtsreihe (Abbildung 2) zeichnet sich durch einen Fokus auf Förderstrategien aus und differenziert in Basis- und Regelfassung mit vielfältigen, selbstdifferenzierenden Aufträgen (Lawrence-Brown 2004). Etwa 80% der Basisfassung ist auch in der Regelfassung enthalten, um gemeinsame Besprechungen zu ermöglichen. Explizit bearbeitet werden vier Verstehengrundlagen und das notwendige Basiskönnen, die für Lernschwache mit und ohne sonderpädagogischem Förderbedarf besonders zu beachten sind (Abbildung 2 linke Spalte).

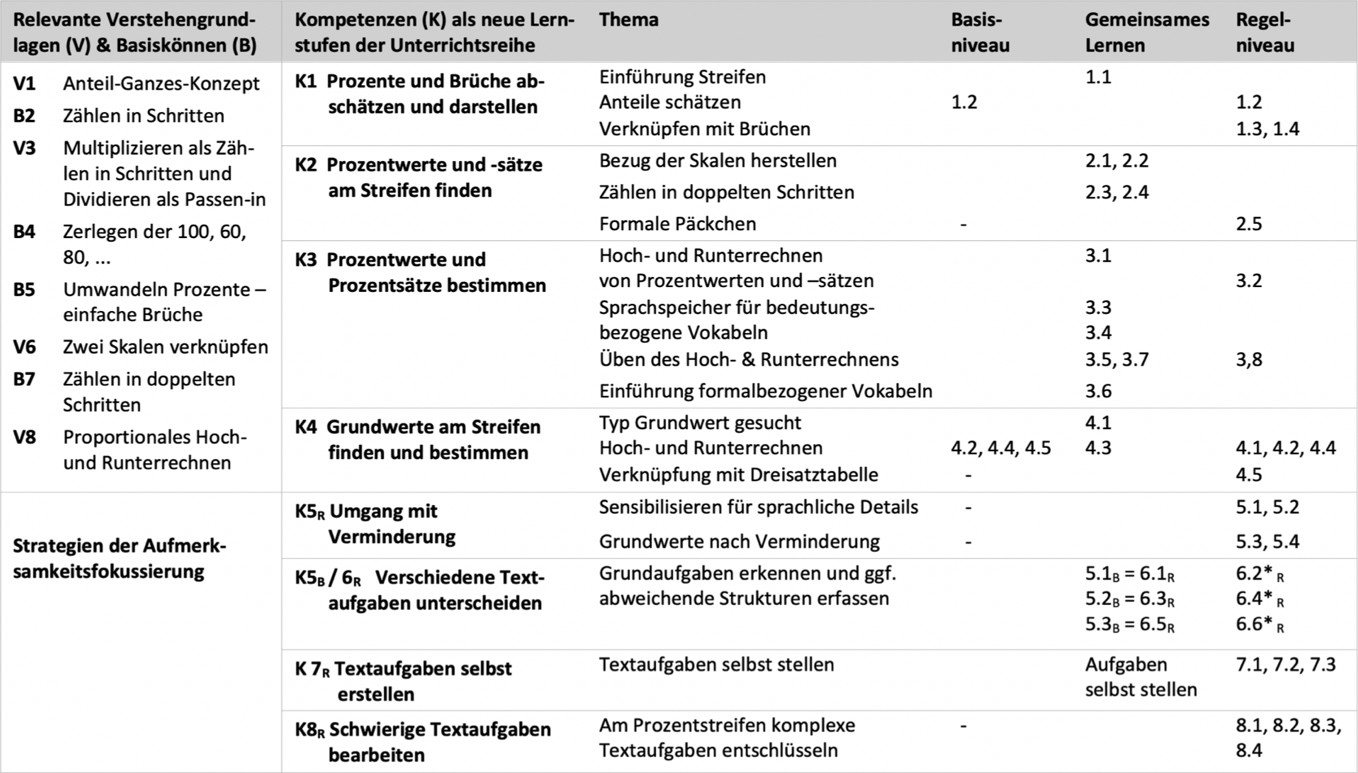
Abbildung 2: Übersicht zur Unterrichtsreihe Prozente verstehen (Pöhler, Prediger und Strucksberg 2018)

Im Rahmen des Forschungsprojektes Matilda wird die auf diese Unterrichtseinheit aufzusetzende Fortbildungsreihe entwickelt und erforscht (vgl. Abbildung 3). Zur didaktisch-methodischen Gestaltung der Fortbildungen kann auf einen soliden Forschungsstand zu Gelingensbedingungen und Wirksamkeit von Gestaltungsprinzipien zurückgegriffen werden (Lipowsky und Rzejak 2017; Timperley et al. 2007). Zentrales Gestaltungsprinzip ist die Verknüpfung von Aktion im Unterricht und Reflexion in der Fortbildung (Clarke und Hollingsworth 2002), hier umgesetzt durch die gemeinsame Bearbeitung der Unterrichtseinheit. Multiprofessionelle Kooperation wird dadurch initiiert, dass sich Regellehrkräfte und Förderlehrkräfte jeweils im Tandem zur Fortbildung anmelden und die Unterrichtseinheit gemeinsam durchführen.

Forschungsmethodisch werden in dem Projekt verschiedene Ansätze und Perspektiven integriert (vgl. Abbildung 3), indem Design-Research auf Unterrichts- und Fortbildungsebene mit einer qualitativen und quantitativen Wirksamkeitsstudie im Prä-Post-Kontrollgruppen-Design verbunden wird. Der vorliegende Artikel fokussiert auf das Teilprojekt 1, die Design-Research-Studie auf Fortbildungsebene, die Darstellung des Teilprojekts 2 erfolgt in anderen Artikeln.

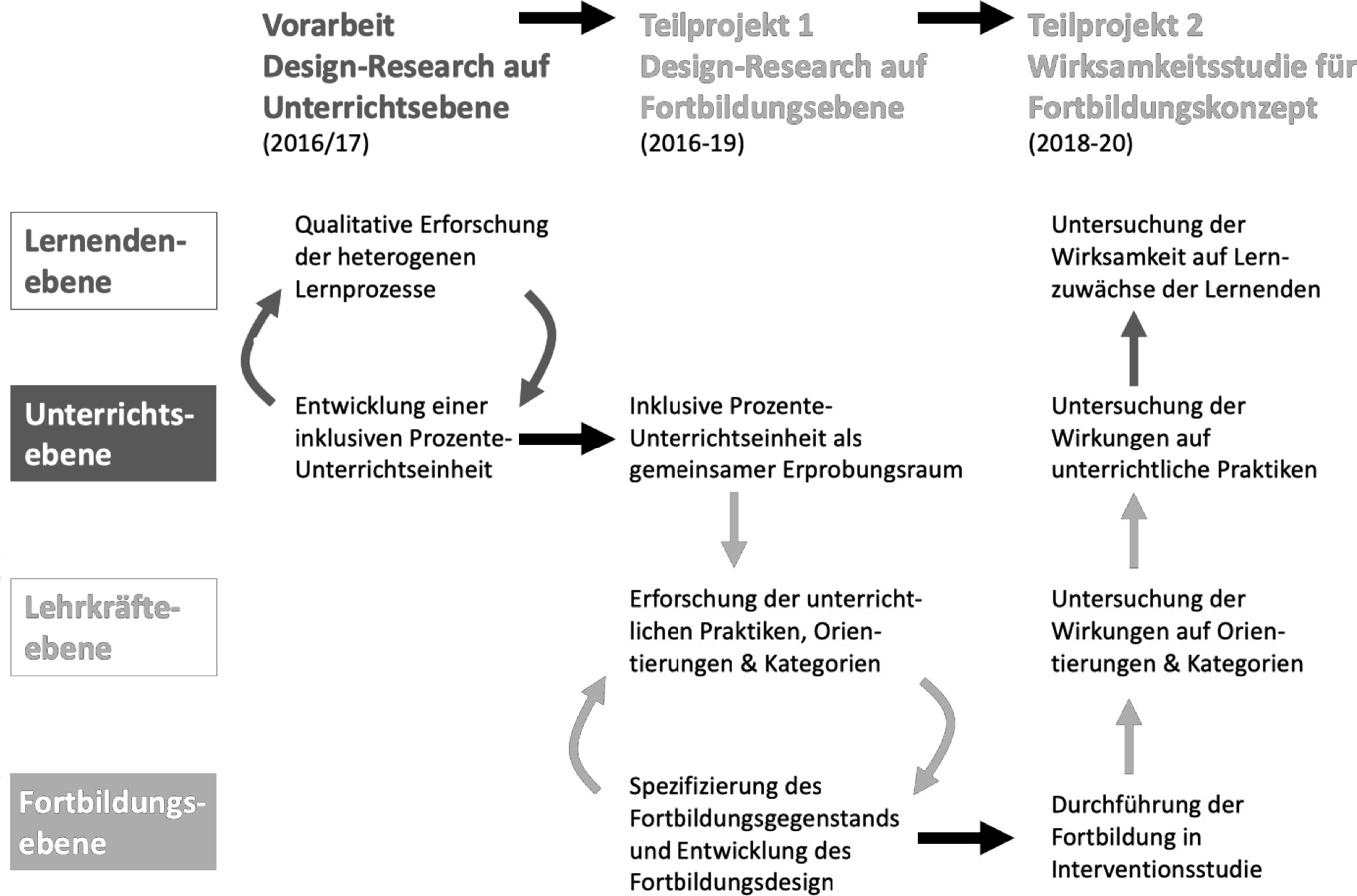
Abbildung 3: Anlage des übergreifenden Forschungsprojekts Matilda

Forschungsdesign und -methoden

Entwicklungsanforderung und Forschungsfrage des Design-Research-Teilprojekts von Matilda

Basierend auf dem derzeitigen Forschungsstand zur Unterrichts- und Fortbildungsebene ergeben sich folgende Forschungsfragen und Entwicklungsanforderungen für ein forschungsbasiertes Fortbildungskonzept:

Forschungsfrage zum IST-Stand: Mit welchen Planungs-, Durchführungs- und Reflexionspraktiken bewältigen Lehrkräfte die unterrichtlichen Anforderungen im inklusiven Unterricht? Welche Orientierungen und Denk- und Wahrnehmungskategorien aktivieren sie dabei implizit oder explizit, und wie sind diese gegenüber dem Forschungsstand zu relationieren?

Entwicklungsanforderung zur Strukturierung des Fortbildungsgegenstands: Wie lassen sich die Fortbildungsgegenstände strukturieren, um Lehrkräfte bei ihren derzeitigen Praktiken, Orientierungen und Kategorien abzuholen und ihr Repertoire im Sinne des Forschungsstands auszudifferenzieren und zu erweitern?

Arbeitsbereiche der gegenstandsbezogenen Design-Research auf Professionalisierungsebene

Die forschungsbasierte Entwicklung des Fortbildungsdesigns einerseits und die entwicklungsbasierte Beforschung der dadurch initiierbaren Planungs- und Reflexionspraktiken von Lehrkräften andererseits erfolgt im Forschungsformat Design-Research, das beide Ziele kombiniert (Cobb et al. 2003). Konkret genutzt wird das Modell der gegenstandsbezogenen Design-Research auf Professionalisierungsebene (Prediger 2019), das vier Arbeitsbereiche iterativ in mehreren Zyklen vernetzt:

Spezifizieren und Strukturieren des Fortbildungsgegenstands,

(Weiter-)Entwickeln eines Fortbildungsdesigns,

Durchführen und Analysieren von Designexperimenten und

(Weiter-)Entwickeln von Beiträgen zur lokalen Theoriebildung zu Fortbildungsgegenständen und -prozessen.

Insbesondere wird auch die Spezifizierung und Strukturierung des Fortbildungsgegenstands durch empirische Analysen angereichert, um in die Gegenstandskonstituierung die Perspektiven von Lehrkräften einzubeziehen (Prediger et al. 2015).

Methoden der Datenerhebung und -auswertung

Um das Unterrichtshandeln der Lehrkräfte mit ihren typischen Anforderungssituationen zu erfassen, wurde die Datenerhebung in drei Designexperiment-Zyklen jeweils sowohl auf Unterrichtsebene als auch auf Fortbildungsebene vorgenommen und durch Interviews mit Planungs- und Reflexionsgesprächen trianguliert.

Auf Unterrichtsebene wurde Vergleichbarkeit des erfassten Unterrichtshandelns hergestellt, indem jeweils auf die gleiche Unterrichtseinheit »Prozente verstehen« fokussiert wurde (vgl. Abschnitt 2.3 und Abbildung 2).

Tabelle 1 gibt einen Überblick zu Zwecken, Stichproben und Datentypen der drei Designexperiment-Zyklen und dem Zusammenspiel von Fortbildungssitzungen, Unterrichtsversuchen der Lehrkräfte und Interviews.

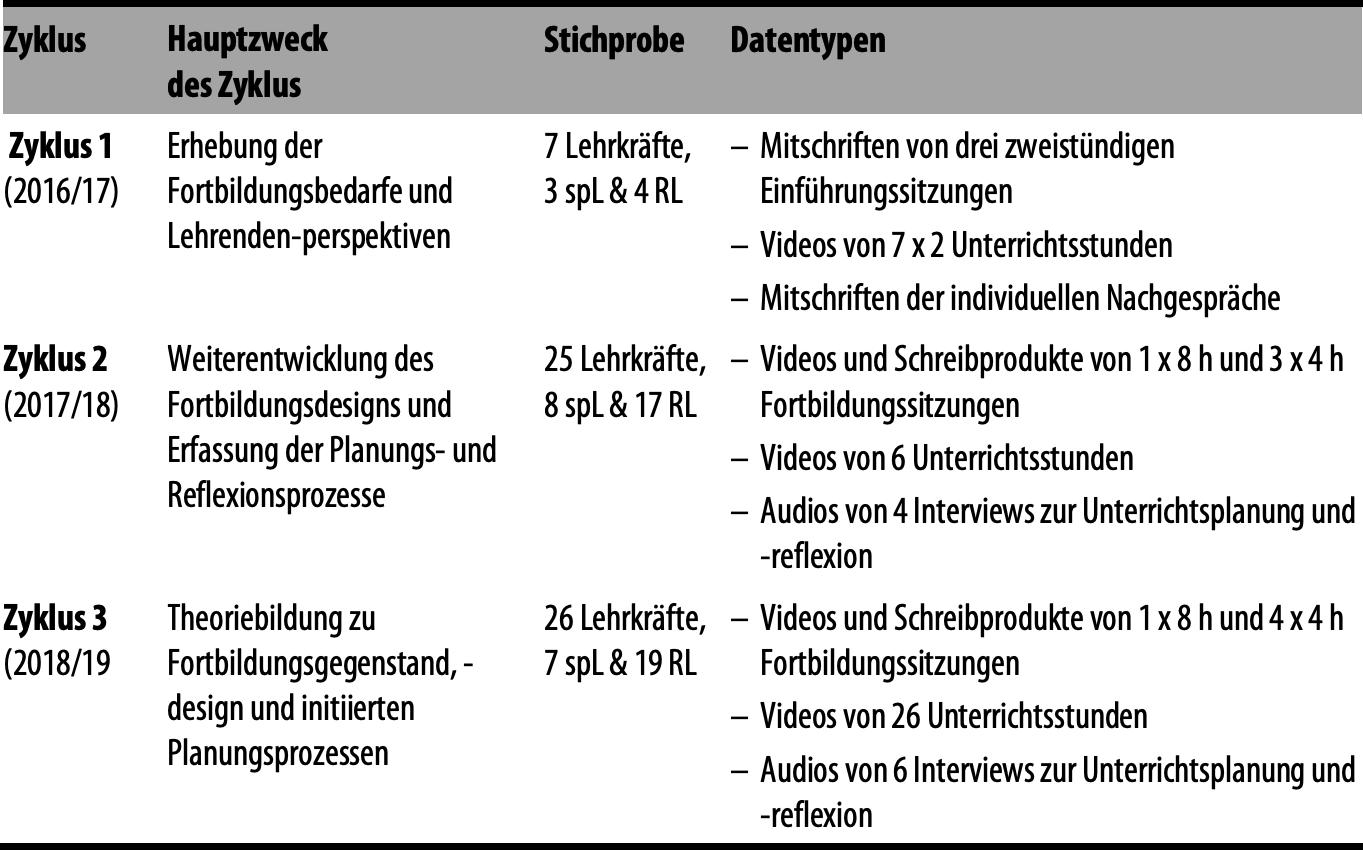
Tabelle 1: Überblick zu den Designexperiment-Zyklen im Projekt Matilda

Zyklus 1 fokussierte auf die Unterrichtspraktiken der Lehrkräfte, um ihre Perspektiven (durch Rekonstruktion der zugrundeliegenden, individuell aktivierten Orientierungen und Denk- und Wahrnehmungskategorien) zu identifizieren und daraus Fortbildungsperspektiven abzuleiten. Die Lehrkräfte wurden jeweils in die Ideen des Unterrichtsmaterials eingeführt und bei ihren konkreten Planungen und Umsetzungen begleitet. In Designexperiment-Zyklus 2 und 3 wurde die vier- bzw. fünfteilige Fortbildungsserie als Minizyklen behandelt, in der die Einsichten in die Planungs- und Reflexionspraktiken der Lehrkräfte während einer Fortbildungssitzung zur Weiterentwicklung der nächsten Sitzung genutzt und durch Planungs- und Reflexionsinterviews ergänzt wurden (Cobb et al. 2003). Der noch laufende Zyklus 3 dient der systematischen Theoriebildung. Insgesamt ist in den drei Zyklen ein Datenkorpus entstanden mit 78 Stunden Unterrichtsvideos von 25 Lehrkräften, 50 Stunden Fortbildungsvideos mit 51 Lehrkräften, diverse Schriftprodukte aus den Arbeitsprozessen und zehn Stunden Audioaufnahmen von Interviews.

So vielfältig wie die Datentypen sind die Methoden zur qualitativen Datenanalyse im Projekt, die alle methodologisch fundiert werden durch das gegenstandsbezogene Expertisemodell nach Bromme (1992). Damit wird jeweils die Expertise der Lehrkräfte qualitativ durch Rekonstruktion der den Planungs-, Moderations- und Reflexionspraktiken zugrundeliegenden, individuell aktivierten Orientierungen und Denk- und Wahrnehmungskategorien erfasst. Sie werden mit dem Forschungsstand abgeglichen, um die Forschungsgegenstände zu perspektivieren (Prediger et al. 2015). Diese wurden in Zyklus 1 und 2 kategorienentwickelnd und hypothesengenerierend mit Methoden der induktiven qualitativen Inhaltsanalyse (Mayring 2015) gewonnen.

In diesem Artikel werden vorrangig Entwicklungsergebnisse aus Zyklus 1 und 2 aufgezeigt und exemplarisch durch empirische Ergebnisse der qualitativen Analysen gestützt. Die zugrundeliegenden Analysen der Protokolle von Unterrichtsbeobachtungen und der Transkripte der individuellen Nachgespräche wurden mittels induktiver qualitativer Inhaltsanalyse entlang von vier Jobs strukturiert, die sich immer wieder als zentral im Lehrkräftehandeln herausgestellt haben: (1) Anforderungen identifizieren, (2) Differenzierte Schwerpunkte setzen, (3) Fokussiert fördern und (4) Gemeinsames Lernen initiieren (siehe Abschnitt 4.1).

Ein forschungsbasiertes Fortbildungskonzept für gegenstandsbezogene Professionalisierung von Lehrkräften zu inklusivem Mathematikunterricht

Um das forschungsbasierte Fortbildungskonzept zu begründen, wird zunächst in Abschnitt 4.1 ein zentrales Ergebnis, die Spezifizierung der Jobs für inklusiven Mathematikunterricht und ihre produktiven Praktiken vorgestellt. Abschnitt 4.2 zeigt exemplarisch an Fallbeispielen, wie die Jobs genutzt werden können, um Professionalisierungsbedarfe von Lehrkräften zu erfassen. Abschnitt 4.3 differenziert diese Jobs mithilfe des Modells der individuellen Lernvoraussetzungen als Grundlage für das zentrale Entwicklungsprodukt, dem Fortbildungskonzept.

Jobs von Lehrkräften für inklusiven Mathematikunterricht

Als zentrales Ergebnis wurden musterhaft wiederkehrende Praktiken und Orientierungen für vier Jobs herauspräpariert. Im Abgleich mit der Forschungsliteratur (vgl. Theorieteil des Artikels) wurden sie in die Kategorien »produktiv« oder »weniger produktiv« für inklusives Lernen eingeteilt, ohne damit den weniger produktiven ihre lokale Plausibilität abzusprechen (vgl. Tabelle 2, Spalte 1 und 2; Literaturhinweise in Spalte 1 verweisen auf empirische Studien, die ebenfalls entsprechende Schwierigkeiten bei Lehrkräften identifiziert haben, Literaturhinweise in Spalte 2 zum Teil auch auf Begründungen, warum diese Praktiken produktiver erscheinen.)

Gegenübergestellt wurden produktive und weniger produktive Praktiken und Orientierungen (gemäß der Charakterisierung von Jackson et al. 2017). Dies erlaubte im nächsten Analyseschritt, für jeden Job diejenigen Denk- und Wahrnehmungskategorien zu identifizieren (Tabelle 2, Spalte 3), die einen Übergang von weniger produktiven zu produktiven Praktiken befördern können. In den Nachgesprächen mit den Lehrkräften wurde kommunikativ validiert, ob sie diese Kategorien tatsächlich aktivieren (operationalisiert nicht durch explizite Benennung oder sogar Bezug zur Literatur, sondern durch Nutzen des zugrundeliegenden Denkmusters in eigenen Worten).

Diese Analyseergebnisse konnten die bestehenden Befunde aus der Literatur gewichten, perspektivieren und integrieren:

Das Bestreben nach Balance von individuellem und gemeinsamen Lernen ist bei vielen Lehrkräften ein lernförderlicher Anknüpfungspunkt, von dem aus die individuellen Professionalisierungsprozesse gestartet werden können (Korff 2015).

Um separierende Zuschreibungen zu überwinden (Prengel 2007), kann das INVO-Modell eine einheitliche Strukturierungen von für alle Kinder relevanten Lernvoraussetzungen bieten (Hasselhorn und Gold 2009).

Beim individuellen Lernen sind Unterstützung- und Förderstrategien zu unterscheiden (Wember 2013).

Die Denkkategorie Lernpfad ermöglicht, beim Differenzieren nicht allein an lokale Anforderungsreduktionen zu denken, sondern an längerfristige Lernprozesse (Feuser 1989; Prediger und von Aufschnaiter 2017).

Um fachliche Anforderungen fachdidaktisch treffsicher zu identifizieren, sind verstehensorientierte Lernpfade notwendig. Daher ist die Denk- und Wahrnehmungskategorie der Verstehensgrundlage zentral (Prediger 2016).

Gemeinsames Lernen verbleibt allein bei sozialer Teilhabe, wenn nicht auch das Voneinander-Lernen auf unterschiedlichen Lernstufen fokussiert wird (Häsel-Weide und Nührenbörger 2013; Wocken 1998).

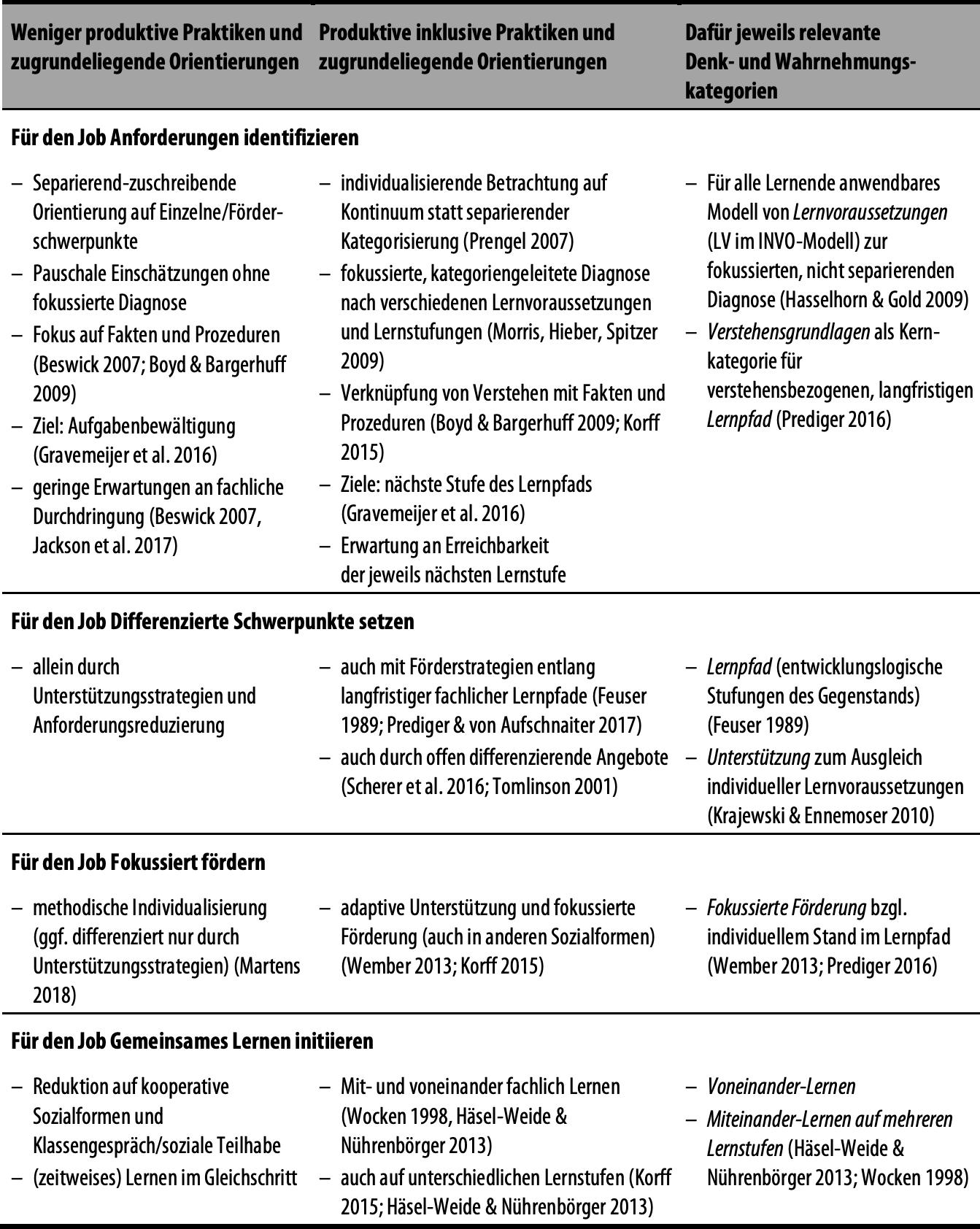
Tabelle 2: Praktiken und Orientierungen mit den jeweils zu explizie­renden Denk- und Wahrnehmungskategorien

Als Konsequenz wurden die aufgeführten Kategorien als zentrale Fortbildungsgegenstände ins Fortbildungsprogramm aufgenommen.

Individuelle Lernstände und Professionalisierungsbedarfe von Lehrkräften

Um die Ergebnisse aus Abschnitt 4.1 zu illustrieren, werden im Folgenden drei Fallbeispiele aus den Planungs- und Reflexionsgesprächen skizziert. Die rekonstruierten Praktiken und Orientierungen zu den vier Jobs erlauben damit eine Identifizierung von individuellen Lernständen und Professionalisierungsbedarfen.

Fallbeispiel 1 – Martina (FL) und Michael (RL)

Martina und Michael unterrichten gemeinsam eine siebte Realschulklasse mit acht Förderkindern (davon drei mit sonderpädagogisch attestierten Förderbedarfen). Obwohl Michael stark nach Förderbedarfen trennt, bleiben seine Beschreibungen der Kinder eher oberflächlich, weil ihm die Sprache fehlt, die jeweiligen Bedarfe zur Förderung genauer zu beschreiben, zum Beispiel: »Paula kommt manchmal mit, vergisst aber vieles wieder«. Martina, die zuvor an einer Förderschule Sprache unterrichtet hat, beschreibt die Kinder dagegen eher auf einem Kontinuum mit vielfältigen Ressourcen und Schwächen. Für heterogene sprachliche Lernstände formuliert sie detailliert differenzierte Schwerpunkte. Die beiden unterrichten am liebsten in zwei heterogenen Halbgruppen parallel, »weil so können alle sozial teilhaben und sich trotzdem in den kleineren Gruppen konzentrieren«. Die Förderkinder werden oft durch entschlackte Aufgaben unterstützt, die stärker vorstrukturiert sind. In Unterrichtsgesprächsphasen achten beide darauf, dass sich zu Beginn alle Lernenden beteiligen und die Schwächeren erst sukzessive aussteigen; sie akzeptieren dies aufgrund der individuell begrenzten metakognitiven Regulation. Andere Lernziele formulieren sie für die offiziell zielgleich zu unterrichtenden Schwachen nicht, auch wenn durch die »zeitdifferenzierende« Beteiligung im Unterrichtsgespräch für die früh Aussteigenden jeweils der Prozess der Abstraktion ausfällt. In der Unterrichtsreihe zum Prozentverständnis sind sie begeistert, wie viel alle Lernenden durch intuitive Zugänge lösen können, fragen sich jedoch nicht, warum der Schritt zur mathematischen Abstraktion stets die gleichen Lernenden abhängt. Sie unterstützen die Aufgabenbewältigung auf differenzierenden Arbeitsblättern durch Adaption auf einfachste Zahlen, sodass alle Lernenden zu Ergebnissen kommen. Prozente können auch die Förderkinder auf diese Weise intuitiv verstehen, der Zugang zum Verständnis der Rechenwege blieb ihnen jedoch versperrt. Gezielt fördern die Lehrkräfte das regelmäßige Sprechen über Anteilsbeziehungen am Prozentstreifen. Alle Lernenden können am Ende in Textaufgaben identifizieren, was der Teil (Prozentwert), was der Anteil (Prozentsatz) und was das Ganze (Grundwert) ist. »Der Prozentstreifen hat uns total gut geholfen, die Leseschwierigkeiten zu überwinden.«

Fallbeispiel 2 – Doris (RL)

Doris unterrichtet an einer neugegründeten Sekundarschule und ist stolz darauf, dass ihr Unterricht durchgängig individualisiert ist. »Mit verschiedenen Arbeitsblättern klappt das super. Alle sind konzentriert am Arbeiten, sogar meine ›Lerner‹ und meistens auch die ›ESE-Kinder‹.« Mit dem angebotenen Unterrichtsmaterial zu Prozenten ist sie nicht glücklich, weil es keine drei Niveaus bietet und die Aufgaben nicht so selbsterklärend sind, dass sie in Einzelarbeit bewältigbar sind. Sie unterstützt ihre Förderkinder, indem sie das Unterrichtsmaterial für sie auf DIN A3 kopiert und einige Aufgabentexte verkürzt. Den Vorschlag der Forscherinnen, mit Kleingruppen moderierte Gespräche über die Verstehenskerne zu führen, probiert sie aus, ist aber nicht zufrieden, denn »so genau wollen die das eh nicht wissen. Ich bin froh, wenn die das dann rechnen können«. Welche Lernfortschritte ihre Lernenden genau machen, kann sie im Reflexionsgespräch nicht sagen. Für die Förderkinder geht sie nach einer Woche doch zum normalen Förderschulbuch über: »Da sind die Aufgaben immer vom gleichen Muster, wenn sie es oft genug üben, können sie das dann irgendwann.« Gemeinsames Lernen heißt bei ihr, dass »die Stärkeren den Schwächeren helfen, wenn sie selbst fertig sind. Das machen die echt nett.«

Fallbeispiel 3 – Carla (FL)

Aus Personalmangel unterrichtet Carla ihre siebte inklusive Gesamtschulklasse allein. Sie analysiert das Unterrichtsmaterial darauf, welche Verstehensgrundlagen hier vorausgesetzt werden und identifiziert das multiplikative Teil-Ganzes-Konzept und die Grundvorstellung der Multiplikation als Zählen in Schritten. »Da weiß ich sofort, dass das meine Spezis nicht können, also müssen wir darauf genau gucken«. Bevor sie mit der Einheit beginnt, wiederholt sie mit der ganzen Klasse das Zählen in Schritten. Die Regelkinder wissen direkt, dass es zum Multiplizieren gehört, für die Förderkinder wird es (wieder) erarbeitet. Für das Kind im Förderschwerpunkt geistige Entwicklung wird eine Annäherung an multiplikatives Denken zum zentralen Lernziel der Unterrichtseinheit. Carla plant ihren Unterricht so, dass die Verstehensgrundlagen in jeder Stunde zur Sprache kommen. Am Ende erzählt sie begeistert: »Gerade für die sehr guten war das toll, denn weil meine Förderkinder immer wieder das Zählen in Schritten mit Multiplizieren verknüpft haben, konnten es die Starken als Begründungsbasis nutzen.«

Damit zeigen sich in den (hier nur grob skizzierten) Fällen typische Beispiele für Praktiken und Orientierungen zu den vier (fett markierten) Jobs: Anforderungen identifizieren, differenzierte Schwerpunkte setzen, Fokussiert fördern und gemeinsames Lernen initiieren (kursiv verweist auf die in Tabelle 2 herausgearbeiteten zentralen Kategorien):

Das Identifizieren von Anforderungen erfolgt bei Martina in Bezug auf die individuellen Lernvoraussetzungen Sprachkompetenz und metakognitiver Regulation, bei Carla in Bezug auf Verstehensgrundlagen als wichtigstes Element des mathematischen Vorwissens. Martin und Doris dagegen diagnostizieren nur in Bezug auf das Arbeitsverhalten, das bei Doris damit auch zum zentralen Qualitätskriterium für das Gelingen des Unterrichts wird (ähnlich bei Breidenstein und Rademacher 2017).

Beim Setzen differenzierter Schwerpunkte beziehen sich Doris, Martina und Michael vorrangig auf Unterstützungsstrategien zum Reduzieren von Anforderungen (bzgl. Arbeitsgedächtnis und metakognitiver Regulation), während Carla die Lernstufungen im langfristigen fachlichen Lernpfad des multiplikativen Verständnisses diagnostiziert und diesbezüglich differenziert. Daher setzt Carla als zentralen mathematischen Schwerpunkt für das Fördern das Verknüpfen von Verstehen mit Prozeduren, während Doris allein die Prozeduren fokussiert.

Für das fokussierte Fördern sehen Michael und Martina zwar Hürden im Verknüpfen von Verstehen und Prozeduren, führen diese jedoch nicht auf fehlende Verstehensgrundlagen zurück und können daher auch nicht gemäß einer Lernstufung fördern. In Bezug auf sprachliche Lernvoraussetzungen nutzt Doris eine Unterstützungs-Ausgleichstrategie, während Martina und Michael sprachliche Lernziele setzen und gerade für die Förderkinder zum zentralen Fördergegenstand machen. Doris interpretiert individuelles Lernen rein unterrichtsmethodisch als Individualisierung, während Martina und Michael (zumindest in Bezug auf sprachliches Lernen) auch fokussierte Förderung vornehmen.

Bezogen auf das gemeinsame Lernen fördert Carla auch in Bezug auf fachliches Lernen und bringt die individuellen Lernstufungen des multiplikativen Denkens auch ins gemeinsame Lernen ein, bei ihr ist Voneinander-Lernen zentral. Damit ist Carla die einzige der sieben Lehrkräfte, die gemeinsames Lernen nicht nur als soziale Teilhabe realisiert, während die anderen beim Miteinander-Lernen stehen bleiben.

Diese Fallbeispiele geben Einblicke in vielfältige Lernstände und Professionalisierungsbedarfe von Lehrkräften. Sie unterscheiden sich nicht nur in der Auswahl der Jobs, die sie sich primär zu eigen machen, sondern auch in ihrer Ausgestaltung, und zwar verschieden für mathematisches Vorwissen, Sprache, Arbeitsgedächtnis und metakognitive Regulation.

Das Fortbildungskonzept im Projekt Matilda

Aus diesen (bei Prediger und Buró, eingereicht, weiter ausgeführten) Beobachtungen zu den Fortbildungsbedarfen der Lehrkräfte zog das Designteam die Konsequenz, die verschiedenen Jobs und Lernvoraussetzungen konsequent zu integrieren, sodass den Lehrkräften ein einheitliches Planungsvorgehen für die verschiedenen mathematikdidaktischen, sprachdidaktischen und sonderpädagogischen Perspektiven angeboten werden kann. Abbildung 4 zeigt, wie die Jobs aus Tabelle 2 für alle relevanten Lernvoraussetzungen parallelisiert und in eine hilfreichere Reihenfolge gebracht wurden: Der zentrale Job in Bezug auf jede der vier Lernvoraussetzungen des INVO-Modells ist, die Anforderungen zunächst gründlich zu identifizieren, bevor sie für einzelne Lernende differenziert und individuell gefördert werden. Da in Bezug auf das Arbeitsgedächtnis eher Unterstützung durch Kompensation als Förderung möglich ist, wurde das Unterstützen im 3. Job integriert.

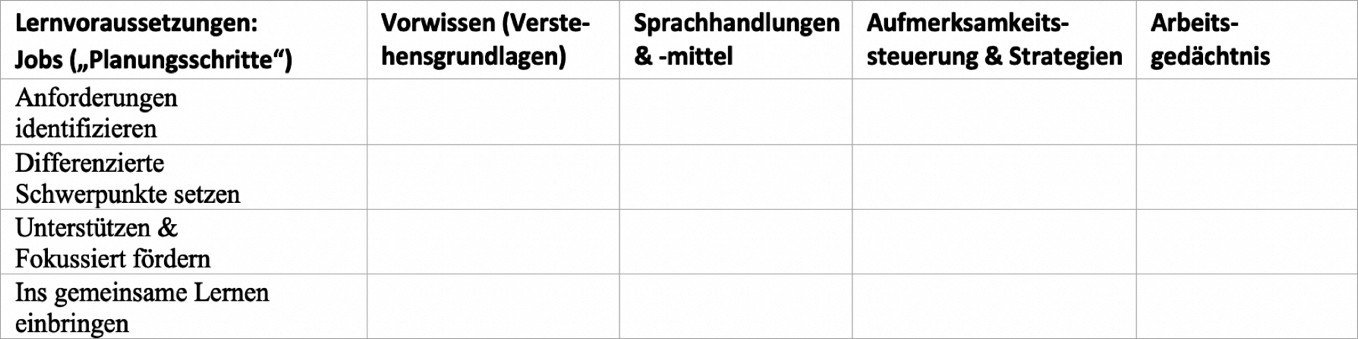
Abbildung 4: Neu strukturierter Fortbildungsgegenstand: Einheitliche Jobs für vier Lernvoraussetzungen des INVO-Modells (Prediger et al. 2019)

Anhand dieser Planungstabelle wurde das Fortbildungskonzept kohärent strukturiert (vgl. Inhaltsüberblick zu den fünf Fortbildungssitzungen in Tabelle 3). Das Streben nach Balance von individuellem und gemeinsamen Lernen wurde als Ausgangspunkt genommen, das INVO-Modell als Kategoriensystem zur Diagnose und Anforderungsidentifizierung in Sitzung 1 eingeführt.

Wie daraus differenzierte Schwerpunkte gesetzt und individuell gefördert werden können, wurde in den weiteren Sitzungen sukzessive erarbeitet, zunächst an anderen Unterrichtsthemen, dann für die Prozente-Einheit. Diese wurde von den Lehrkräften erprobt und zur Reflexion und Festigung der Fortbildungsgegenstände genutzt.

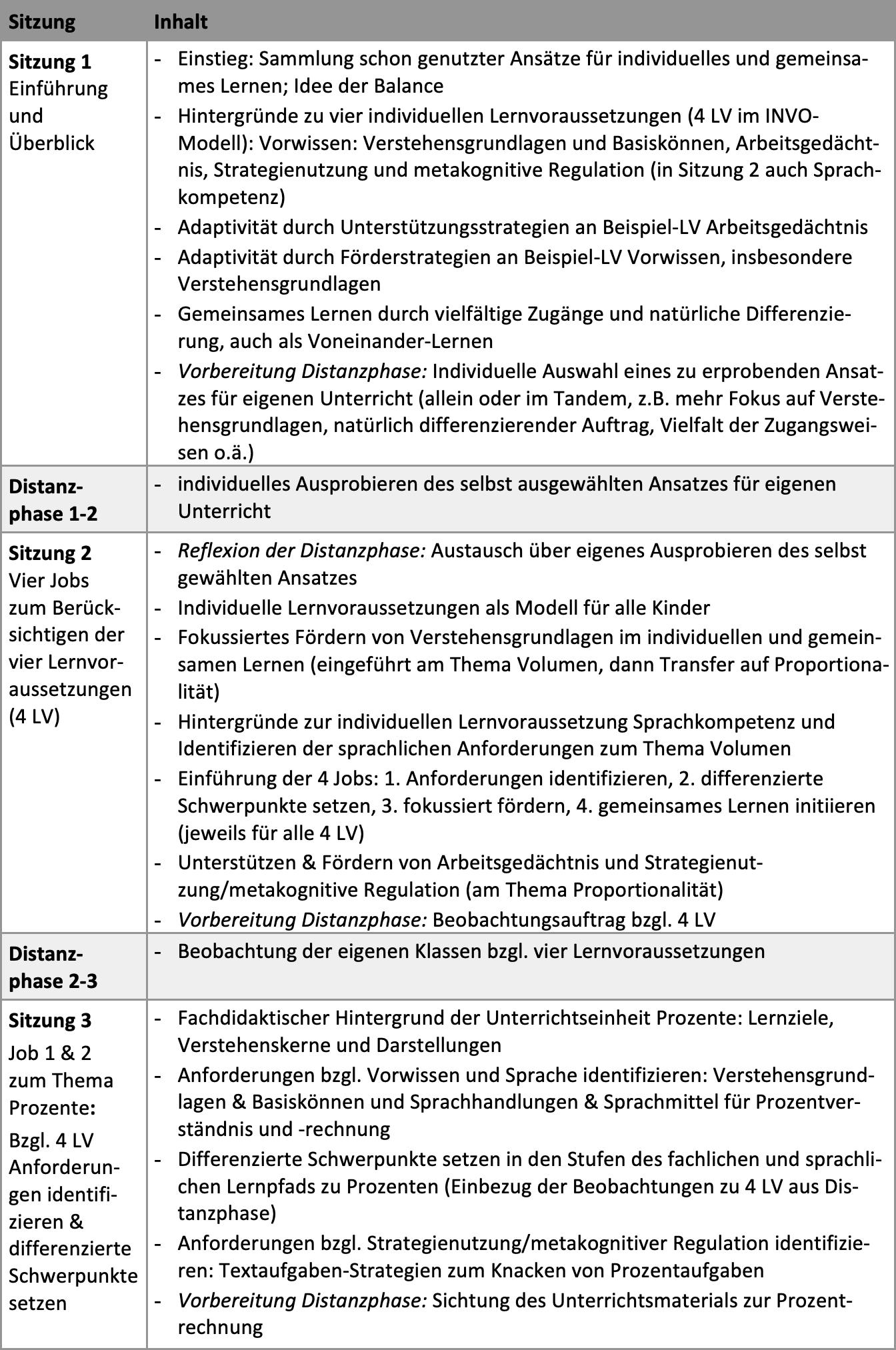
Tabelle 3: Überblick über Inhalte der fünf Fortbildungssitzungen (Entwicklungsergebnis des 2. Zyklus für Hauptstudie im 3. Zyklus)

Ersten Eindrücke aus dem Fortbildungsdurchgang zeigen, dass die Integration der Perspektiven mit dem einheitlichen Model der Planungsschritte für vier Lernvoraussetzungen (Abbildung 4) für die Lehrkräfte eine hilfreiche Strukturierung zu bieten scheint, um über zu einfache Differenzierungsstrategen herauszukommen und tatsächlich auf unterschiedliche Lernstufungen zu fokussieren. Damit scheint auch das fokussierte Fördern zielsicherer zu gelingen. Die Organisation gemeinsamen Lernens auf unterschiedlichen Lernstufen dagegen erweist sich als höchste Lernstufe auf den Lernpfaden der Lehrkräfte, die nur eine Minderheit bereits erreicht. Trotz der Komplexität der Planungstabelle in Abbildung 4 gelang es einigen Lehrkräften dennoch, ihren Unterricht entlang einer differenzierten Schwerpunktsetzung und einer Balance von individuellem und gemeinsamen Lernen auszurichten. Allerdings meldeten viele Lehrkräfte zurück, dass sie die Kategorien und Jobs selten gleichzeitig berücksichtigen konnten. Es wurde in den Analysen ihrer Planungs-, Durchführungs- und Reflexionspraktiken deutlich, dass sie jeweils nur auf kleine Teilbereiche zugriffen und sich die zugrundeliegende Gesamtvision von inklusivem Fachunterricht erst schrittweise zu eigen machten (Buró und Prediger 2019; Büscher 2019).

Diskussion und Ausblick

Für die Qualitätsentwicklung im inklusiven Fachunterricht der Sekundarstufe 1 liegen bereits bewährte Unterrichtskonzepte und substanzielle empirische Befunde aus Psychologie, Sonderpädagogik und Fachdidaktik vor. Diese sind bislang allerdings kaum interdisziplinär integriert und zu handlungsnahen Fortbildungskonzepten aufbereitet worden. Während die Aufbereitung vor allem eine Selektion relevanter Denk- und Wahrnehmungskategorien aus der Vielzahl theoretisch verfügbarer erfordert, ist ihre Integration in ein handlungsnahes Modell ausgesprochen anspruchsvoll.

Im vorgestellten Projekt Matilda wurde dazu ein (drei Zyklen umfassendes) Design-Research-Projekt durchgeführt, um ausgehend von qualitativen Rekonstruktionen der Planungs-, Durchführungs- und Reflexionspraktiken von Lehrkräften zu ermitteln, welche Orientierungen den produktiven und weniger produktiven Praktiken zugrunde liegen und welche Denk- und Wahrnehmungskategorien für eine Weiterentwicklung notwendig sind (vgl. Tabelle 2, empirisch ausführlicher in Prediger und Buró eingereicht). Auch wenn die Analysen hier nur andeutungsweise vorgestellt werden konnten, wird damit eine Forschungsbasierung für die Spezifizierung und Strukturierung des Fortbildungsgegenstands geschaffen.

Insgesamt zeigt sich, dass inklusive Unterrichtspraktiken für Lehrkräfte eine große Herausforderung darstellen, weil sie die Integration vielfältiger Jobs, Orientierungen und Wissensbestände aus verschiedenen Bezugsdisziplinen erfordern. Diese Integration bildet eine Entwicklungsherausforderung, für die ein interdisziplinär zusammengesetztes Design-Team drei Zyklen brauchte, bevor es eine befriedigende Lösung produzieren konnte. Das dabei entwickelte, einheitliche Modell für Planungsschritte für vier Lernvoraussetzungen (Abbildung 4) bewährt sich anscheinend gut, wie erste (noch weiter zu vertiefende) Analysen zeigen.

Im nächsten Schritt des Entwicklungsforschungsprojekts Matilda werden die qualitativen Analysen vertieft, die Lernprozesse der Lehrkräfte dabei genauer untersucht und schließlich die Wissenszuwächse und Veränderung der Orientierungen auch quantitativ in einem Prä-Post-Kontrollgruppendesign untersucht. Dabei wird die Entwicklung der Fortbildungsgruppe im Vergleich zu einer Materialgruppe, die lediglich das Unterrichtsmaterial und Handreichung ohne Fortbildung erhält, und einer Kontrollgruppe, die eine Prozenteinheit nach eigenen Vorstellungen ohne weitere Unterstützung durchführt, erfasst (vgl. Abbildung 3).

Förderhinweis: Das Projekt Matilda – Mathematik inklusiv lehren lernen wird finanziert vom BMBF (Förderkennzeichen 01NV1704, Projektleitung S. Prediger und J. Kuhl). Es ist erwachsen aus dem Forschungskontext des Deutschen Zentrums für Lehrerbildung Mathematik (DZLM, finanziert durch die Deutsche Telekom-Stiftung) und einer Kooperation im Rahmen des Projekts DoProfil (in der Qualitätsoffensive Lehrerbildung). Wir danken Judith Strucksberg, Claudia Ademmer, Claudia Wittich und Imke Pulz für die Kooperation.

Literatur

Beswick, Kim. 2007. »Influencing Teachers’ Beliefs About Teaching Mathematics for Numeracy to Students with Mathematics Learning Difficulties.« Mathematics Teacher Education and Development 9: 3–20.

Boyd, Brian, und Mary Ellen Bargerhuff. 2009. »Mathematics Education and Special Education: Searching for Common Ground and the Implications for Teacher Education.« Mathematics Teacher Education and Development 11: 54–67.

Breidenstein, Georg, und Sandra Rademacher. 2017. Individualisierung und Kontrolle: Empirische Studien zum geöffneten Unterricht in der Grundschule. Wiesbaden: Springer.

Bromme, Rainer. 1992. Der Lehrer als Experte. Bern: Huber.

Buró, Sarah, und Susanne Prediger. 2019. »Low entrance or reaching the goals? Mathematics teachers’ categories for differentiating with open-ended tasks in inclusive classrooms.« In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, herausgegeben von Uffe Thomas Jankvist, Marja van den Heuvel-Panhuizen und Michiel Veldhuis, 4636—4643. Utrecht: Freudenthal Group und ERME.

Büscher, Christian. 2019. »Conceptual learning opportunities in teachers’ differentiated task designs for inclusive mathematics education.« In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, herausgegeben von Uffe Thomas Jankvist, Marja van den Heuvel-Panhuizen und Michiel Veldhuis, 3604-3611. Utrecht: Freudenthal Group und ERME.

CAST. 2011. Universal Design for Learning Guidelines version 2.0. Wakefield, MA: Author. http://www.udlcenter.org/sites/udlcenter.org/files/UDL_Guidelines_Version_2.0_(Final)_3.doc (Zugriff: 20.08.2015).

Clarke, David J., und Hilary Hollingsworth. 2002. »Elaborating a model of teacher professional growth.« Teaching and Teacher Education 18 (8): 947–967.

Cobb, Paul, Jere Confrey, Andrea diSessa, Richard Lehrer und Leona Schauble. 2003. »Design Experiments in Educational Research.« Educational Researcher 32(1): 9–13.

Döbert, Hans, und Horst Weishaupt, Hrsg. 2013. Inklusive Bildung professionell gestalten. Situationsanalyse und Handlungsempfehlungen. Münster: Waxmann.

Ennemoser, Marco, Kristin Krajewski und Sabrina Schmidt. 2011. »Entwicklung und Bedeutung von Mengen-Zahlen-Kompetenzen und eines basalen Konventions- und Regelwissens in den Klassen 5 bis 9.« Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 43: 228–242.

Feuser, Georg. 1989. »Allgemeine integrative Pädagogik und entwicklungslogische Didaktik.« Behindertenpädagogik 28 (1): 4–48.

Gersten, Russell, David J. Chard, Madhavi Jayanthi, Scott K. Baker, Paul Morphy und Jonathan Flojo. 2009. »Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components.« Review of Educational Research 79 (3): 1202–1242.

Gravemeijer, Koeno, Geeke Bruin-Muurling, Jean-Marie Kraemer und Irene van Stiphout. 2016. »Shortcomings of Mathematics Education Reform in The Netherlands« Mathematical Thinking and Learning 18 (1): 25–44.

Häsel-Weide, Uta, und Marcus Nührenbörger. 2013. »Mathematiklernen im Spiegel von Heterogenität und Inklusion.« Mathematik differenziert 4 (2): 6–8.

Hasselhorn, Marcus, und Andreas Gold. 2009. Pädagogische Psychologie. Erfolgreiches Lernen und Lehren. Stuttgart: Kohlhammer.

Jackson, Kara, Lynsey Gibbons und Charlotte Sharpe. 2017. »Teachers’ views of students’ mathematical capabilities: Challenges and possibilities for ambitious reform.« Teachers College Record 119 (7): 1–43.

Jandl, Sarah. 2016. Mathematikspezifisches Professionswissen von Sonderpädagoginnen und Sonderpädagogen. Zürich: Universität Zürich.

Korff, Natascha. 2015. Inklusiver Mathematikunterricht in der Primarstufe. Baltmansweiler: Schneider Hohengehren.

Krajewski, Kristin. 2013. »Wie bekommen Zahlen einen Sinn: ein entwicklungspsychologisches Modell der zunehmenden Verknüpfung von Zahlen und Größen.« In Rechenstörungen bei Kindern: Neurowissenschaft, Psychologie, Pädagogik, herausgegeben von Michael von Aster und Jens H. Lorenz, 155–179. Göttingen: Vandenhoeck & Ruprecht.

Krajewski, Kristin, und Marco Ennemoser. 2010. »Die Berücksichtigung begrenzter Arbeitsgedächtnisressourcen in Unterricht und Lernförderung.« In Brennpunkte der Gedächtnisforschung herausgegeben von Hans-Peter Trolldenier, Wolfgang Lenhard und Peter Marx, 337–365. Göttingen: Hogrefe.

Kuhl, Jan. 2019. Beschreiben und Verändern – Sonderpädagogik als werteorientierte und reflektierte Wirkungsforschung. Vierteljahresschrift für Heilpädagogik und ihre Nachbargebiete Plus, 88 (1): 1–13.

Kuhl, Jan, Teresa Hecht und Nils Euker. 2016. »Grundprinzipien des Unterrichts und der Förderung von Kindern und Jugendlichen mit intellektueller Beeinträchtigung.« In Evidenzbasierte Diagnostik und Förderung von Kindern und Jugendlichen mit intellektueller Beeinträchtigung, herausgegeben von Jan Kuhl und Nils Euker, 39–64. Bern: Hogrefe.

Kuhl, Jan, Daniel Sinner und Marco Ennemoser. 2012. »Training quantity-number competencies in students with intellectual disabilities.« Journal of Cognitive Education and Psychology 11 (2): 128–142.

Kutzer, Reinhard. 1999. »Überlegungen zur Unterrichtssituation im Sinne strukturorientierten Lernens.« In Mit Behinderungen muss gerechnet werden, herausgegeben von Holger Probst, 15–69. Solms-Oberbiel: Jarick.

Lawrence-Brown, Diana. 2004. »Differentiated Instruction: Inclusive Strategies for standard-based learning that benefit the whole class.« American Secondary Education 32 (3): 34–62.

Lipowsky, Frank, und Daniela Rzejak. 2017. »Fortbildungen für Lehrkräfte wirksam gestalten.« Bildung und Erziehung 70 (4): 379–399.

Lütje-Klose, Birgit. 2012. »Sprachlich-kommunikative Beeinträchtigungen bei Schülerinnen und Schülern mit dem Förderschwerpunkt Lernen.« In Sprache und Kommunikation. Enzyklopädisches Handbuch der Behindertenpädagogik, Band 8, herausgegeben von Otto Braun und Ulrike Lüdtke, 646–652. Stuttgart: Kohlhammer.

Lütje-Klose, Birgit, Susanne Miller und Holger Ziegler. 2014. »Professionalisierung für die inklusive Schule als Herausforderung für die LehrerInnenbildung.« Soziale Passagen 6 (1): 69–84.

Martens, Matthias. 2018. »Individualisieren als unterrichtliche Praxis.« In Unterricht beobachten – beschreiben – rekonstruieren, herausgegeben von Matthias Proske und Kerstin Rabenstein, 207–222. Bad Heilbrunn: Klinkhardt.

Mayring, Philipp. 2015. »Qualitative content analysis: Theoretical background and procedures.« In Approaches to qualitative research in mathematics education, herausgegeben von Angelika Bikner-Ahsbahs, Christine Knipping und Norma Presmeg, 365–380. Dordrecht: Springer.

Melzer, Conny, Clemens Hillenbrand, David Sprenger und Thomas Hennemann. 2015. »Aufgaben von Lehrkräften in inklusiven Bildungssystemen – Review internationaler Studien.« Erziehungswissenschaft 26 (51): 61–80.

Misquitta, Radhika. 2011. »A review of the literature: Fraction instruction for struggling learners in mathematics.« Learning Disabilities Research & Practice 26 (2): 109–119.

Morris, Anne K., James Hiebert und Sandy M. Spitzer. 2009. »Mathematical Knowledge for Teaching in Planning and Evaluating Instruction« Journal for Research in Mathematics Education 40 (5): 491–529.

Moser Opitz, Elisabeth. 2007. Rechenschwäche/Dyskalkulie. Bern: Haupt.

Moser Opitz, Elisabeth, Okka Freesemann, Susanne Prediger, Urs Grob, Ina Matull und Stephan Hußmann. 2017. »Remediation for Students With Mathematics Difficulties« Journal of Learning Disabilities 50 (6): 724–736.

Moser, Vera, und Andreas Kropp. 2014. Abschlussbericht: Kompetenzen in inklusiven setting (KIS) – Vorarbeiten zu einem Kompetenzstrukturmodell sonderpädagogischer Lehrkräfte. Berlin: Humboldt-Universität.

Pöhler, Birte. 2018. Konzeptuelle und lexikalische Lernpfade und Lernwege zu Prozenten. Wiesbaden: Springer Spektrum.

Pöhler, Birte, Susanne Prediger und Judith Strucksberg. 2018. Prozente verstehen – Inklusive Unterrichtseinheit in Basis- und Regelfassung. Open Educational Ressource. Zugänglich unter sima.dzlm.de/um.

Prediger, Susanne. 2016. »Inklusion im Mathematikunterricht: Forschung und Entwicklung zur fokussierten Förderung statt rein unterrichtsmethodischer Bewältigung.« In Befähigung zu gesellschaftlicher Teilhabe, herausgegeben von Jürgen Menthe, Dietmar Höttecke, Thomas Zabka, Marcus Hammann und Martin Rothgangel, 361–372. Münster: Waxmann.

Prediger, Susanne. 2019. »Promoting and investigating Teachers’ Pathways towards Expertise for Language-Responsive Mathematics Teaching.« Mathematics Education Research Journal 31 (4): 367–392. doi:10.1007/s13394-019-00258-1.

Prediger, Susanne, und Sarah Buró. 2020, eingereicht. »Selbstberichtete Praktiken von Lehrkräften zu Anforderungssituationen des inklusiven Mathematikunterrichts – Eine Interviewstudie« Eingereicht beim Journal für Mathematikdidaktik.

Prediger, Susanne, Judith Strucksberg, Claudia Ademmer, Birte Pöhler, Jan Kuhl, Claudia Wittich, et al. 2019. Matilda-Handreichung zum inklusiven Prozente-Unterricht. Open Educational Ressource aus dem Projekt Mathematik inklusiv lehren lernen. Dortmund: Technische Universität/DZLM.

Prediger, Susanne, Uta Quasthoff, Anna-Marietha Vogler und Vivien Heller. 2015. »How to elaborate what teachers should learn? Five steps for content specification of professional development programs.« Journal für Mathematik-Didaktik 36 (2): 233–257.

Prediger, Susanne, und Claudia von Aufschnaiter. 2017. »Umgang mit heterogenen Lernvoraussetzungen aus fachdidaktischer Perspektive: Fachspezifische Anforderungs- und Lernstufungen berücksichtigen.« In Studienbuch Umgang mit Heterogenität in Schule und Unterricht, herausgegeben von Thorsten Bohl, Jürgen Budde und Markus Rieger-Ladich, 291–307. Bad Heilbrunn: Kinkhardt.

Prengel, Annedore. 2007. »Diversity Education – Grundlagen und Probleme der Pädagogik der Vielfalt.« In Diversity studies. Grundlagen und disziplinäre Ansätze, herausgegeben von Gertraude Krell, Barbara Riedmüller, Barbara Sieben und Dagmar Vinz, 49–67. Frankfurt/M.: Campus.

Ratz, Christoph. 2009. Aktiv-entdeckendes Lernen bei Schülern mit geistiger Behinderung. Oberhausen: Athena.

Scherer, Petra, Kim Beswick, Lucie DeBlois, Lulu Healy und Elisabeth Moser Opitz. 2016. »Assistance of students with mathematical learning difficulties: how can research support practice?« ZDM Mathematics Education 48 (5): 633–649.

Schuppener, Saskia. 2014. »Inklusive Schule – Anforderungen an Lehrer_innenbildung und Professionalisierung.« Zeitschrift für Inklusion-online 1–2. http://www.inklusion-online.net/index.php/inklusion-online/article/view/220/221.

Scruggs, Thomas E., und Margo A. Mastropieri. 1996. »Teacher Perceptions of Mainstreaming/Inclusion, 1958–1995: A Research Synthesis.« Exceptional Children 63 (1): 59–74.

Sinner, Daniel, und Jan Kuhl. 2010. »Förderung mathematischer Basiskompetenzen in der Grundstufe der Schule für Lernhilfe.« Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie 42 (4): 241–251.

Spörer, Nadine, Kai Maaz, Miriam Vock, Agi Schründer-Lenzen und Thorsten Luka. 2015. »Lernen in der inklusiven Grundschule« Unterrichtswissenschaft 43 (1): 22–35.

Timperley, Helen, Aaron Wilson, Heather Barrar und Irene Fung. 2007. Teacher professional learning. Best Evidence Synthesis Iteration. Wellington: Ministry of Education.

Tomlinson, Carol Ann. 2001. How to differentiate instruction in mixed-ability classrooms. Alexandria: Association for Supervision and Curriculum Development.

Wember, Franz. 2013. »Herausforderung Inklusion.« Zeitschrift für Heilpädagogik 64 (10): 380–388.

Wild, Elke, Malte Schwinger, Birgit Lütje-Klose, Sittipan Yotyodying und Julia Gorges. 2015. »Schülerinnen und Schüler mit dem Förderschwerpunkt Lernen in inklusiven und exklusiven Förderarrangements.« Unterrichtswissenschaft 43 (1): 7–21.

Wocken, Hans. 1998. »Gemeinsame Lernsituationen.« In Integrationspädagogik, herausgegeben von Anne Hildeschmidt und Irmtraud Schnell, 37–52. München: Juventa.

Die Autorinnen und Autoren

Susanne Prediger, Prof. Dr., ist seit 2006 Professorin für Mathematikdidaktik am Institut für Entwicklung und Erforschung des Mathematikunterrichts und seit 2017 Vize-Direktorin am Deutschen Zentrum für Lehrerbildung Mathematik. Ihr Forschungsschwerpunkt ist Professionalisierungsforschung und Umgang mit Heterogenität im Mathematikunterricht.

Kontakt: prediger@math.tu-dortmund.de

Jan Kuhl, Prof. Dr., ist seit 2015 Professor für Unterrichtsentwicklungsforschung mit dem Schwerpunkt Inklusion. Sein Forschungsschwerpunkt ist die Entwicklung, Evaluation und Implementierung von Konzepten der Diagnostik und evidenzbasierten Förderung im inklusiven Unterricht.

Kontakt: jan.kuhl@tu-dortmund.de

Christian Büscher, Dr., ist seit 2014 wissenschaftlicher Mitarbeiter am Institut für Entwicklung und Erforschung des Mathematikunterrichts. Er untersucht Professionalisierungsprozesse von Lehrkräften zum inklusiven Mathematikunterricht.

Kontakt: christian.buescher@tu-dortmund.de

Sarah Buró ist Doktorandin und seit 2017 wissenschaftliche Mitarbeiterin am Institut für Entwicklung und Erforschung des Mathematikunterrichts. Sie untersucht dazu Professionalisierungsprozesse von Lehrkräften zum inklusiven Mathematikunterricht.

Kontakt: sarah.buro@math.tu-dortmund.de